Quaternions I: Overview

What are quaternions? Let's start with what quaternions once were: an attempt to extend Complex numbers to three dimensions.

Back when the geometric interpretation of complex numbers as a plane was reasonably fresh, Sir William Hamilton became interested in finding a system of algebra that would allow him to express three dimensional space in the same way. To do this, Hamilton needed a way to add and multiply points in 3 dimensional space together.

Addition came easy. Picking some arbitrary origin and axes 1, i, and j to work with, Hamilton just defined (a + bi +cj) + (d + ei +fj ) = ( a + d ) + ( b + e )i + ( c  + f )j.

Multiplication, though, was a problem. Assuming that these new quantities were distributive, Hamilton needed to define ij in such a way that various other properties still held. Despite his best efforts, he couldn't do it.

SPLASH!

These are all the materials I used/planned to use in class. I'll also put some links below for topics/sites I find interesting. Hope it helps! If you leave comments, I can try to get back to you and direct you to resources.
Happy Coding!
~Will

Where to go in order to...

• Install Python
• Install Notepad++ (A good text editor for working with python on windows. On Linux/Mac, you should be able to use whatever you have on hand.)
• Learn Python
• Do fun problems!

Stuff I wrote for the class (I'm planning on teaching this class again next year, so I may write more worksheets...):

• Expressing the (almost) Infinite
• Project Euler Problems

Neat Topics

• http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
• http://en.wikipedia.org/wiki/Collatz_conjecture
• http://en.wikipedia.org/wiki/Genetic_algorithm
• and more...

Imaging Exoplanets: Out of this world pictures

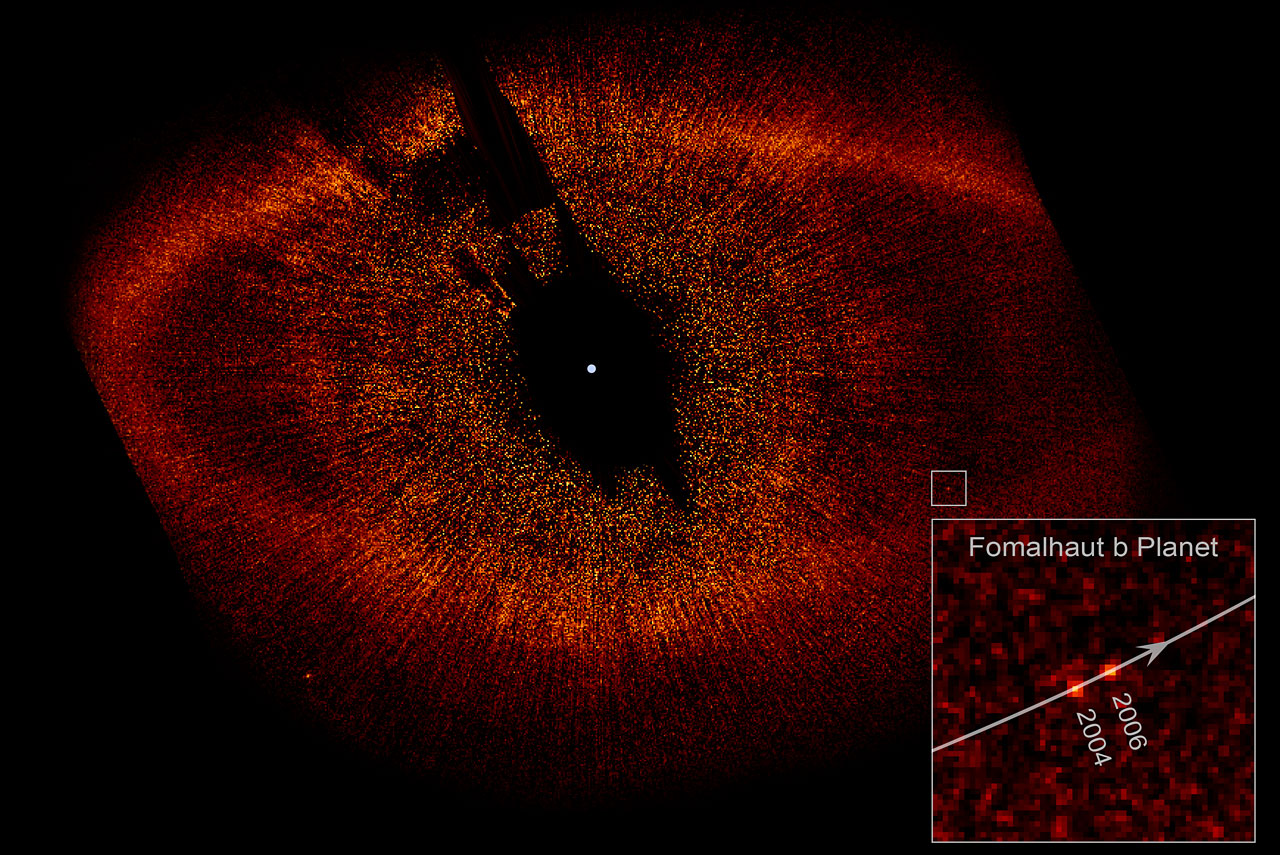   Back in 2008, the image at left was plastered across the front page of many science related publications. For the first time, scientists had directly imaged an exoplanet (a planet which orbits another star) with visible light.
   Exoplanets themselves were nothing new.  In late 2008, 333 exoplanet canidates were known, and 8 of those had been detected using direct imaging. In fact, Fomalhaut b itself, the planet pictured, was actually not truly a new discovery. Since 2004 scientists had been reasonably confident it existed because of the sharp inner edge of the band of dust around the star Formalhaut. The thought was that a large planet (namely Fomalhaut b) was sweeping the material from the inside of the band into itself.